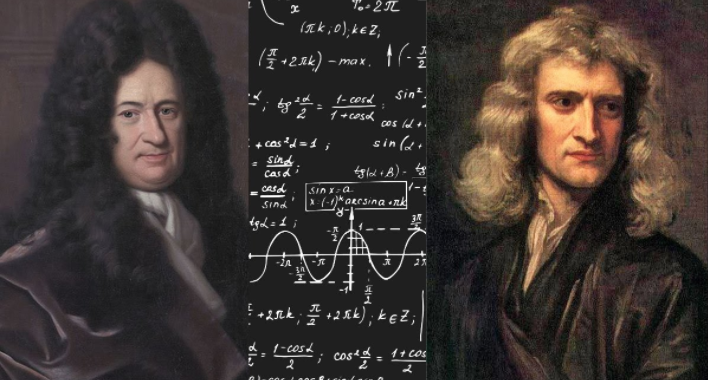By Angela Zhu
Many high school students struggle with learning Math, especially Calculus. But when they get to know the “story behind the scenes”, calculus can no longer be a monster. In this article, we will explore the story of the famous Calculus Controversy and the basic theories of calculus.

The Newton-Leibniz Calculus Controversy
Calculus was primarily introduced by two scientists: Issac Newton and Gottfried Wilhelm Leibniz. However, Newton is the one most often credited with this development. This story of “who got there first” is called the Newton-Leibniz Calculus Controversy, which takes place in the mid-1660s.
At that time, Newton claimed that he invented this system, and wrote several papers that he refused to publish. The reason for not publishing his papers was unknown, but the fact that he did circulate them to his friends and used the technique discovered in his scientific works proved that these papers existed. His first paper on Calculus was said to be written in 1669.
Leibniz, however, performed the research himself, devised this idea in the mid-1670s, and published his work in 1684. The name of the paper is known as “A New Method for Maxima and Minima, as Well Tangents, Which is not Obstructed by Fractional or Irrational Quantities”. Although the work was extremely obscure and difficult to understand, the title of his paper is a great summary of the basic idea of calculus.
The controversy between these two mathematicians began in the 1770s: When Newton realized that Leibniz had developed a similar idea, he sent a letter to Leibniz to ensure that he would receive the credit for this, and even made accusations that Leibniz read some of his manuscripts to develop his own idea. But, since the paper of Leibniz was published first, people were confused about who “stole” the idea from the other. This controversy further impeded the progress of mathematics in Britain as mathematicians didn’t utilize the developing system of calculus in their research.

Differentiation and Integration
After talking about the Newton-Leibniz Controversy, we have to talk about what calculus is exactly. According to the definition proposed by thegreatcoursesdaily.com, calculus is a specialized mathematics that allows one to calculate the behaviour of functions as they near points close to infinity. It is the study of the relationships of limits, integrals, and derivatives. It is hard to understand it without having basic knowledge of differentiation and integration, which includes the terminologies mentioned in the definition.
Differentiation is a way to find the rate of change of a function, known as the derivative. To find the rate of change of a certain point on that function, the slope of the tangent line going through this point must be calculated. Therefore, by finding the derivative of the whole function, we can obtain its slope at any point by plugging in the numbers. The 3 basic derivatives are:
- (n is a real number) D(x^n) = nx^(n − 1)
- (Trigonometric functions) D(sin x) = cos x and D(cos x) = −sin x
- (Exponential functions) D(e^x) = e^x
Chain rules and other properties can also be used on complex functions.
 Integration, on the other hand, is the method used to calculate the area formed by the curve, and it can further be used to find the volume of a solid. By slicing the area or the solid into an infinite number of known areas, such as rectangles, circles or disks, and “add” them together, the result can easily be obtained. Below is the notation of integration. The integral of the integrand, which is the function, is the antiderivative, the opposite of the derivative.
Integration, on the other hand, is the method used to calculate the area formed by the curve, and it can further be used to find the volume of a solid. By slicing the area or the solid into an infinite number of known areas, such as rectangles, circles or disks, and “add” them together, the result can easily be obtained. Below is the notation of integration. The integral of the integrand, which is the function, is the antiderivative, the opposite of the derivative.

The Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is the most well-known definition of calculus. Below is the most common version of this theorem.

There is a continuous function f and we have a new function for the area under the curve defined as y=f(t).
In this version, the derivative of F is f, so in other words, the antiderivative of f is F. This theorem weaves the differential and integral calculus together, by clearly stating how to find the area under a curve by using antidifferentiation.
Calculus is an essential tool for both academic and professional purposes. It can improve the quality of the final product, and ensure that it is safe to use. For example, in Engineering, Medical science, Physics, Research Analysis, etc. Moreover, it is the language of scientists, economists and engineers; it is very involved in and can greatly influence our daily lives.

[author] [author_image timthumb=’on’]https://drive.google.com/file/d/1GtzU1D5vZ76UAOvIwTS7SHpE0rZKlOGB/view?usp=sharing[/author_image] [author_info]Angela is a Grade 11 student at The Study in Westmount, Quebec. I love Engineering, Math and Biology, and I am fascinated by how these subjects can be connected together. I like exploring and learning new STEM concepts, and reading the latest STEM news! In my spare time, I enjoy playing tennis, skiing, reading and watching anime![/author_info] [/author]
References:
- “Who Invented CALCULUS: Newton OR LEIBNIZ?” The Great Courses Daily, 24 June 2020, www.thegreatcoursesdaily.com/invented-calculus-newton-leibniz/.
- Calculus i – the Definition of the Derivative, tutorial.math.lamar.edu/classes/calci/defnofderivative.aspx.
- “Introduction to Integration.” Math Is Fun, www.mathsisfun.com/calculus/integration-introduction.html.
- “Fundamental Theorem of Calculus Review (Article).” Khan Academy, Khan Academy, www.khanacademy.org/math/in-in-grade-12-ncert/xd340c21e718214c5:definite-integrals/xd340c21e718214c5:fundamental-theorem-of-calculus-chain-rule/a/fundamental-theorem-of-calculus-review.
- “Home.” The Great Courses Daily, 16 Sept. 2021, www.thegreatcoursesdaily.com/.
Images:
- “Who Invented CALCULUS: Newton OR LEIBNIZ?” The Great Courses Daily, 24 June 2020, www.thegreatcoursesdaily.com/invented-calculus-newton-leibniz/.
- “When i Starts Solving Differentiation and Integration Meme.” AhSeeit, 15 Mar. 1970, ahseeit.com/hindi/?qa=6918%2Fwhen-starts-solving-differentiation-and-integration-meme.
- Rio Grande City CISD Grulla High School. Rio Grande City CISD Grulla High School – Daniel Lopez, ghs.rgccisd.org/205616_2.
- “Keep Calm and Pass Calculus.” Like This Poster, keepcalms.com/p/keep-calm-and-pass-calculus/